Subscribe | Instructors | Students | Texts & Study Guides | Contact Us | Home
Current Subscribers:
Intro Macro | Intro Micro | Password Reminder
| Subscribe to Intro Micro | About Intro Micro | Intro Micro Sample Site |

They say "the rich get richer and the poor get poorer" meaning that the inequality in the distribution of wealth grows. For the last half of the 1990s the rich have gotten richer, and the other 90% have fared worse. In fact, according to some estimates, the distribution is so unequal that the top 1% may have as much as half of the total wealth. As the distance between the 'haves' and 'have nots' grows, the 'haves' have been buying and building mansions at a rate that is faster than at any time since the 1920s.
The increase in the demand for mansions is being driven by a rapid increase in both the number of wealthy households in the U.S. and in the amount of wealth held by these households. Just as an increase in income shifts out demand for luxury goods, so does an increase in wealth. A household's wealth, or net worth, is the net value of everything it owns (cash+stocks+bonds+property - debts = wealth).
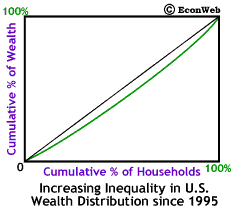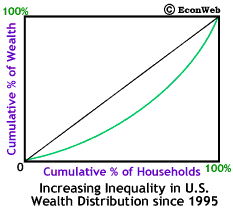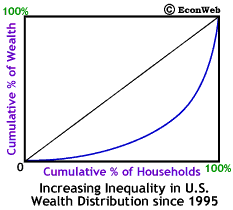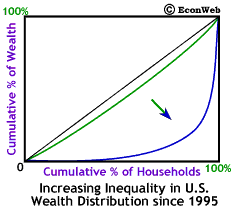
Since 1995, the number of households with net worth in excess of $US 1 million has increased by a third, to over 4 million households; the rate of increase in households with net wealth over $US 10 million is even greater. However, the same increases in wealth have not accrued to the rest of the U.S. population. While the wealthiest 10% are better off than before, the other 90% of U.S. households have seen their wealth fall. The run-up of the stock market over the last few years has lead to greater inequality in the distribution of wealth in the U.S. This is shown (in exaggerated form) by an increased bowing out of the Lorenz curve, shown to the right. Click here for more information on the Lorenz curve and the Gini coefficient.
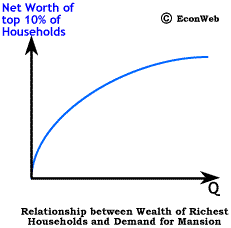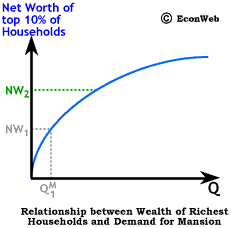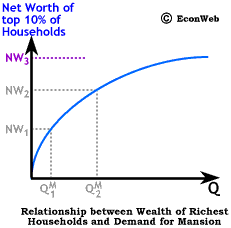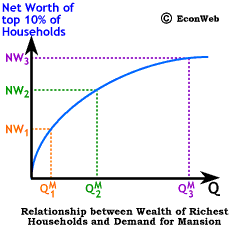
To the right, we show the equivalent of an Engel curve for mansion demand by wealthy households, or what we might call a wealth demand curve for mansions. The shape shows that demand for mansions increases at an increasing rate as the wealth of the already wealthiest households increases. This curve shows a wealth elasticity of demand for mansions that is greater than 1, meaning, that as the wealth of the richest households increases, the demand for mansions increases at a greater rate. The increase in wealth from NW1 to NW2 is roughly the same as from NW2 to NW3, however the increase in demand from Q2 to Q3 is far larger than the increase from Q1 to Q2. This increasing rate of demand can be interpreted not just as an increase in the number of mansions, but the cost and size as well. As wealth continues to increase, so does the size of what is considered to be an adequate mansion. An absurd example might be Aaron Spelling's (you know... Tori's dad) mansion which, among other niceties such as multiple pools and tennis courts, is purported to have 3 rooms set aside just for wrapping gifts.
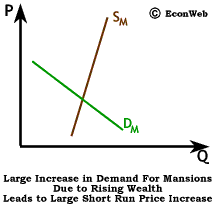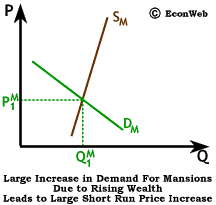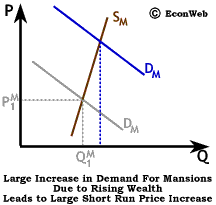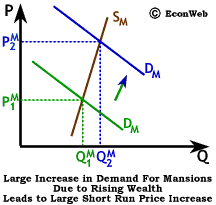
Because as wealth increases, demand for luxury goods increases at a faster rate, the demand for mansions has risen rapidly in the last few years. The impact on the market for luxury housing in the short run is shown to the right by a large shift up in demand for mansions due to an increase in wealth. Demand rises rapidly, but short-run supply is very inelastic for mansions (because they require many months to be built). The result is a rapid increase in the price of luxury housing. In parts of the U.S. where wealthy households are more concentrated, like the Silicon Valley area, it's common to hear stories about houses offered for sale at $US 2 million which actually sell for $US 3 million in one day as an excess of wealthy would-be mansion owners bid the price up. Because supply is inelastic in the short run, the price rises very rapidly, but quantity cannot.
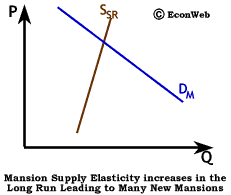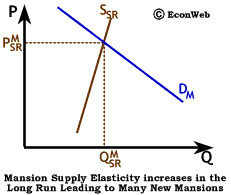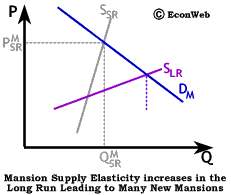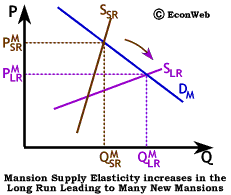
The longer-run effect on the market is somewhat different. As the number of wealthy households continues to increase, and as demand continues to grow, the construction industry has time to react by building more luxury housing, and the supply of mansions becomes more elastic. With more elastic long-run supply, the number of mansions is able to increase significantly and the price is able to fall. Almost 10,000 homes were sold for over $US 1 million in the U.S. in 1998. In some cities, the demand for mansions close to downtown business centers has made empty lots more valuable than those lots with middle-class homes, because of the extra cost involved in tearing down a home before construction of a new mansion can begin.
As is the case for any other good, if demand is driven up rapidly in a market with inelastic supply, price increases quickly. Over time, supply becomes more elastic, leading to a decrease in price and an increase in quantity. The rich may be different from the rest of us, but the market for luxury items isn't so different from any other market.
| Subscribe to Intro Micro | About Intro Micro | Intro Micro Sample Site |